The Seven Bridges Of Königsberg: A Journey Through Mathematical History

The Seven Bridges of Königsberg: A Journey Through Mathematical History

Related Articles: The Seven Bridges of Königsberg: A Journey Through Mathematical History

Introduction

With great pleasure, we will explore the intriguing topic related to The Seven Bridges of Königsberg: A Journey Through Mathematical History. Let’s weave interesting information and offer fresh perspectives to the readers.

The Seven Bridges of Königsberg: A Journey Through Mathematical History

The Seven Bridges of Königsberg problem, a seemingly simple question about traversing a city’s bridges, holds a profound place in the history of mathematics. It is credited with being the genesis of graph theory, a branch of mathematics that has found widespread applications in computer science, social networks, and even the study of the human brain.

The Problem:

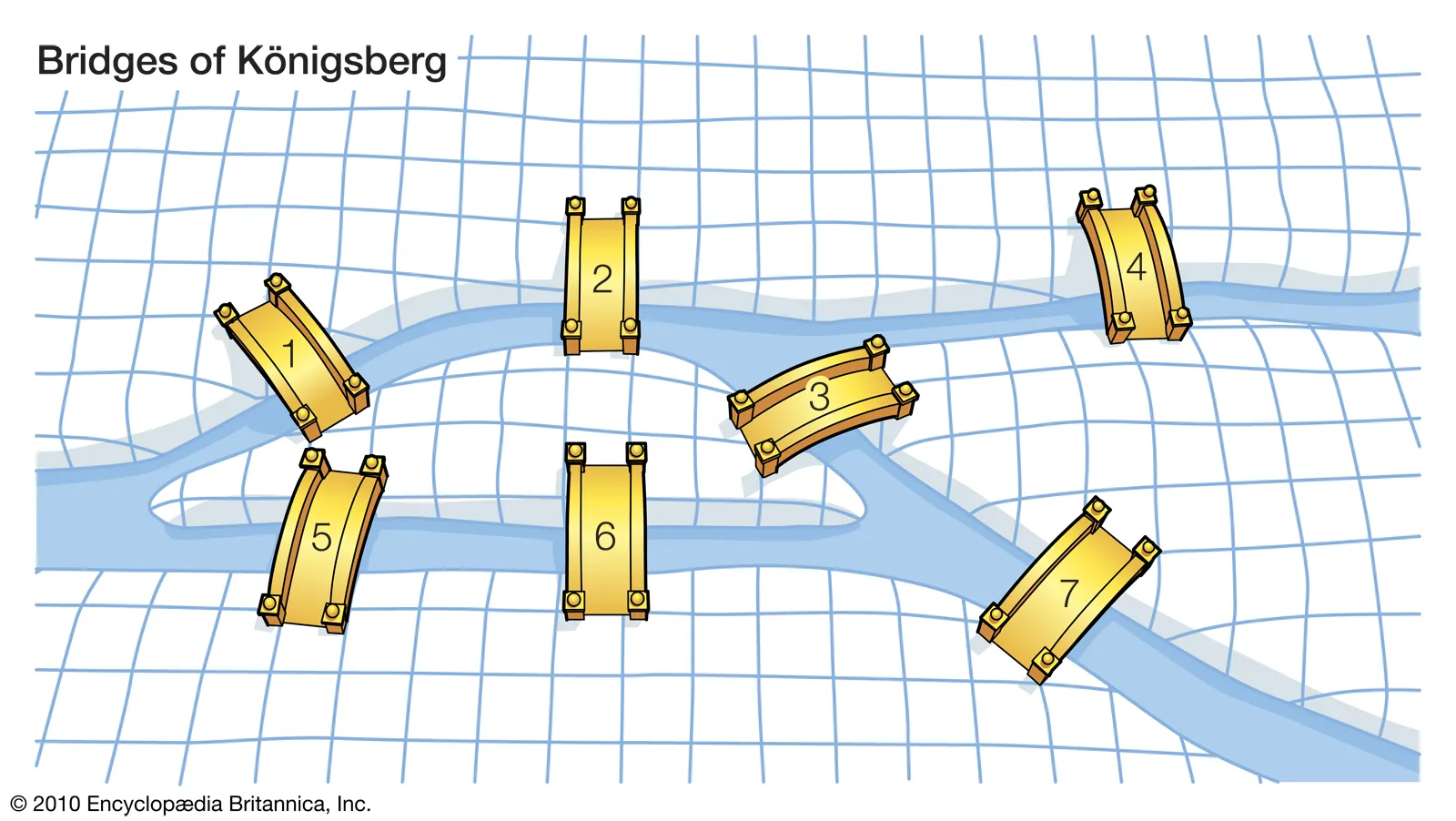
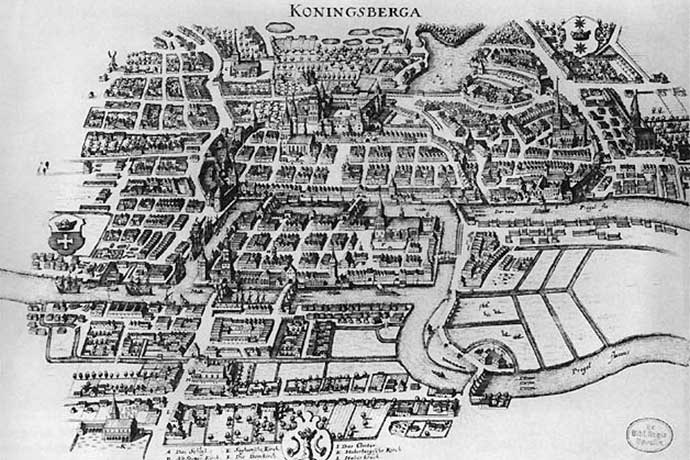
Königsberg, a city in Prussia (now Kaliningrad, Russia), was built on the Pregel River, with seven bridges connecting its four landmasses. The city’s residents enjoyed leisurely walks, often attempting to find a route that crossed each bridge exactly once. The challenge, however, proved insurmountable. No one could find a solution, and the question of whether such a route existed became a local curiosity.

Euler’s Solution:

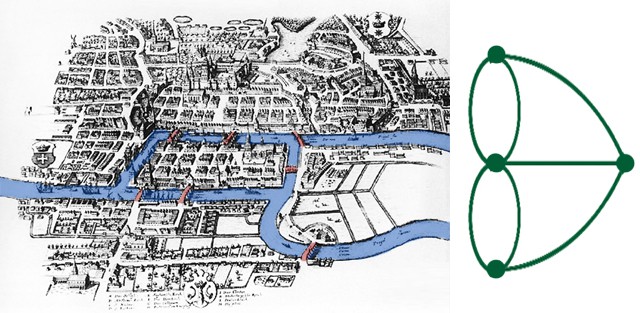
In 1736, Leonhard Euler, a renowned Swiss mathematician, addressed the problem. He recognized that the essence of the puzzle lay not in the specific shape of the landmasses or the bridges, but in their connections. He abstracted the problem, representing each landmass as a point (vertex) and each bridge as a line connecting two points (edge). This abstraction resulted in a graph, a fundamental concept in graph theory.

Euler’s groundbreaking insight was that the existence of a route traversing all bridges exactly once depended on the number of edges connected to each vertex. He observed that a vertex with an odd number of edges would have to be either the starting or ending point of the route, as a route entering the vertex would require an exit edge. Consequently, a route traversing all bridges exactly once is possible only if there are at most two vertices with an odd number of edges.

In the case of Königsberg, all four landmasses had an odd number of bridges, thus violating the condition. Euler proved that no such route existed, conclusively answering the city’s long-standing question.

The Legacy of Königsberg:

Euler’s solution to the Seven Bridges of Königsberg problem was a significant turning point in mathematical history. It marked the birth of graph theory, a field that has since blossomed into a powerful tool for analyzing and understanding complex relationships.

The applications of graph theory are vast and diverse:

• Computer Science: Graph theory is crucial in computer science, particularly in algorithm design, network analysis, and data structures. It is used to model computer networks, optimize routing algorithms, and understand the structure of data.

• Social Networks: The study of social networks relies heavily on graph theory to analyze relationships between individuals, identify influential nodes, and understand the spread of information.

• Biology and Chemistry: Graph theory finds applications in analyzing molecular structures, understanding protein interactions, and modeling biological networks.

• Transportation and Logistics: Graph theory is used in optimizing transportation networks, planning routes, and managing logistics operations.

The Seven Bridges of Königsberg Today:

The Seven Bridges of Königsberg, while no longer a puzzle, remains a powerful symbol of the potential of abstract thinking. The problem’s transformation into a mathematical graph demonstrates the power of abstraction in revealing underlying patterns and solving complex problems.

FAQs about the Seven Bridges of Königsberg:

• Q: Is it possible to walk across all seven bridges of Königsberg exactly once?

  A: No, it is not possible. Euler proved that no such route exists.

• Q: Why is the Seven Bridges of Königsberg problem important?

  A: It is considered the birth of graph theory, a fundamental branch of mathematics with widespread applications in various fields.

• Q: What is graph theory?

  A: Graph theory is the study of graphs, which are mathematical structures used to represent relationships between objects. Graphs consist of vertices (points) and edges (lines connecting vertices).

• Q: What is the main concept behind Euler’s solution?

  A: Euler’s solution relies on the concept of vertex degree, which is the number of edges connected to a vertex. A route traversing all edges exactly once is possible only if there are at most two vertices with an odd degree.

• Q: What are some applications of graph theory?

  A: Graph theory has applications in computer science, social networks, biology, chemistry, transportation, and logistics.

Tips for Understanding the Seven Bridges of Königsberg:

• Visualize the problem: Draw a simple diagram representing the landmasses and bridges as points and lines.

• Focus on connections: Understand that the key to the solution lies in the connections between the landmasses, not their specific shapes.

• Think about vertex degree: Pay attention to the number of edges connected to each vertex (landmass).

• Explore the concept of Eulerian circuits: An Eulerian circuit is a route that traverses all edges of a graph exactly once.

• Research further: Explore the history of graph theory and its diverse applications in various fields.

Conclusion:

The Seven Bridges of Königsberg problem, though seemingly simple, holds a profound significance in the history of mathematics. It marked the birth of graph theory, a powerful tool for understanding and analyzing complex relationships. Euler’s solution to the problem, while seemingly straightforward, revealed the power of abstract thinking and the potential of mathematical concepts to address real-world challenges.

The Seven Bridges of Königsberg, a seemingly simple puzzle, has transcended its historical context and continues to inspire mathematicians and computer scientists alike, leaving a lasting legacy in the world of mathematics.

Closure

Thus, we hope this article has provided valuable insights into The Seven Bridges of Königsberg: A Journey Through Mathematical History. We appreciate your attention to our article. See you in our next article!