Unlocking The Power Of Dimensionality Reduction: Understanding UMAP’s Neighborhoods

Unlocking the Power of Dimensionality Reduction: Understanding UMAP’s Neighborhoods

Related Articles: Unlocking the Power of Dimensionality Reduction: Understanding UMAP’s Neighborhoods

Introduction

With enthusiasm, let’s navigate through the intriguing topic related to Unlocking the Power of Dimensionality Reduction: Understanding UMAP’s Neighborhoods. Let’s weave interesting information and offer fresh perspectives to the readers.

Unlocking the Power of Dimensionality Reduction: Understanding UMAP’s Neighborhoods

In the realm of data analysis, navigating complex, high-dimensional datasets can be akin to traversing a dense forest with limited visibility. Dimensionality reduction techniques, like Uniform Manifold Approximation and Projection (UMAP), offer a powerful solution by transforming intricate datasets into lower-dimensional representations while preserving essential relationships. UMAP achieves this by identifying and leveraging the inherent structure of the data, particularly through its concept of "nearest neighbors."

The Essence of Neighborhoods in UMAP

At its core, UMAP operates on the principle of finding local neighborhoods within the data. It assumes that data points close to each other in the high-dimensional space are likely to be similar and should remain close in the reduced space. These "nearest neighbors" are determined by measuring the distances between data points using a chosen distance metric, such as Euclidean distance or Manhattan distance.

Building a Faithful Representation: The Importance of Nearest Neighbors

The concept of nearest neighbors plays a crucial role in UMAP’s ability to create faithful low-dimensional representations. By preserving the local neighborhood structure, UMAP ensures that the relationships between data points are accurately reflected in the reduced space. This preservation of local structure is essential for tasks such as:

• Clustering: Identifying groups of similar data points, even in high-dimensional spaces, becomes more efficient and accurate when local relationships are maintained.
• Visualization: UMAP enables the visualization of high-dimensional data, allowing for the identification of patterns and outliers that might be hidden in the original space.
• Anomaly Detection: By understanding the local neighborhood structure, UMAP can effectively identify data points that deviate significantly from their neighbors, potentially signaling anomalies.
• Data Exploration: UMAP facilitates the exploration of complex datasets by providing a simplified view that highlights the key relationships and patterns within the data.

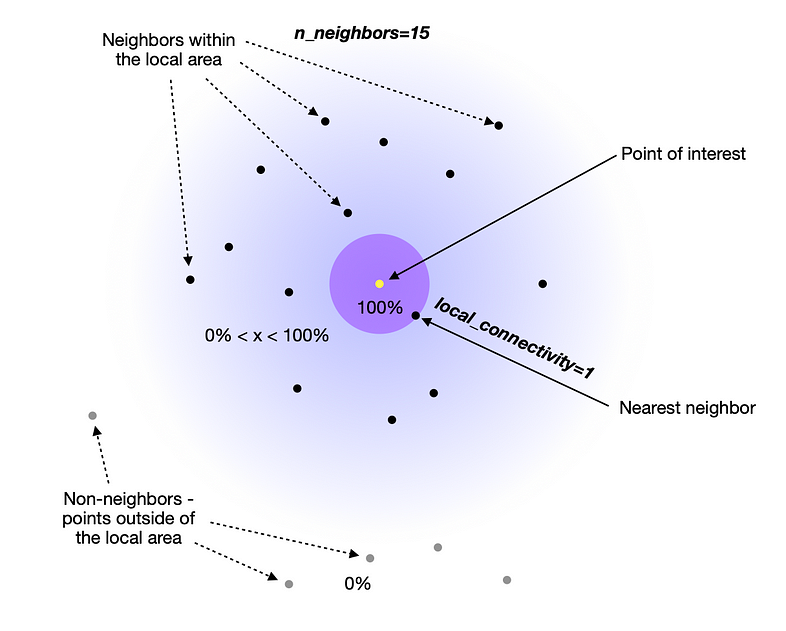
The Mechanics of Neighbor Identification: K-Nearest Neighbors and Epsilon-Neighborhoods

UMAP offers two primary methods for determining nearest neighbors:

1. K-Nearest Neighbors (KNN): This method identifies the "k" data points closest to a given point, where "k" is a user-defined parameter. The value of "k" dictates the size of the neighborhood, with larger "k" values resulting in broader neighborhoods.

2. Epsilon-Neighborhoods: This method defines a neighborhood based on a distance threshold, known as "epsilon." All data points within this distance threshold are considered neighbors. The choice of "epsilon" determines the size of the neighborhood, with larger "epsilon" values encompassing more neighbors.

The choice between these methods depends on the specific characteristics of the dataset and the desired outcome. KNN is often favored for its simplicity and intuitive nature, while epsilon-neighborhoods can be more effective for datasets with varying densities.

Beyond the Neighborhood: Connecting the Dots with Graph Construction

Once the nearest neighbors are identified, UMAP constructs a graph representation of the data. This graph, known as a "k-nearest neighbor graph" or an "epsilon-neighborhood graph," captures the relationships between data points within their respective neighborhoods. Each data point becomes a node in the graph, and edges connect neighboring points.

This graph serves as a fundamental structure for UMAP’s subsequent dimensionality reduction process. The algorithm leverages the connections within the graph to create a low-dimensional embedding that preserves the local neighborhood structure.

Fine-Tuning the Embedding: The Role of Local and Global Structure

UMAP’s ability to create faithful representations hinges on its ability to balance the preservation of local and global structure. The local structure, as defined by the nearest neighbors, is crucial for capturing the immediate relationships between data points. However, the global structure, which encompasses the overall relationships within the data, is equally important for achieving an accurate embedding.

UMAP achieves this balance through a combination of techniques:

• Local Neighborhood Preservation: The graph construction and embedding process prioritize the preservation of local relationships, ensuring that neighboring points in the high-dimensional space remain close in the reduced space.
• Global Structure Preservation: UMAP employs a technique called "fuzzy simplicial sets" to capture the global structure of the data. This technique allows for the representation of overlapping neighborhoods, providing a more nuanced understanding of the relationships between data points.
• Hyperparameters: UMAP offers a range of hyperparameters that can be adjusted to fine-tune the embedding process. These parameters include the "number of neighbors," "minimum distance," and "embedding dimension," allowing users to tailor the embedding to their specific needs.

Addressing Common Questions about UMAP and Its Neighborhoods

1. How do I choose the appropriate number of neighbors (k) or epsilon value for my dataset?

The choice of "k" or "epsilon" depends on the characteristics of the dataset and the desired outcome. For datasets with clear clusters, a smaller "k" or "epsilon" might be appropriate, as it emphasizes the local structure and helps to distinguish between clusters. Conversely, for datasets with less defined clusters, a larger "k" or "epsilon" might be necessary to capture the broader relationships between data points.

2. Can UMAP handle datasets with varying densities?

UMAP is designed to handle datasets with varying densities. By using epsilon-neighborhoods, UMAP can adapt to the local density of the data, ensuring that the neighborhood size is appropriate for different regions of the dataset.

3. How does UMAP handle outliers?

Outliers can pose challenges for dimensionality reduction techniques, as they often deviate significantly from the general structure of the data. UMAP addresses this by using a "minimum distance" parameter, which helps to prevent outliers from unduly influencing the embedding process.

4. How can I evaluate the quality of the UMAP embedding?

The quality of the UMAP embedding can be evaluated using various metrics, such as the "neighborhood preservation" score, which measures the extent to which the local neighborhood structure is preserved in the reduced space. Visual inspection of the embedding can also provide insights into its quality, particularly for identifying any potential distortions or misrepresentations.

Tips for Effective UMAP Implementation

1. Preprocessing: Before applying UMAP, consider preprocessing the data to ensure that it is suitable for dimensionality reduction. This might involve scaling the data, handling missing values, or removing irrelevant features.
2. Hyperparameter Tuning: Experiment with different hyperparameter values to find the optimal configuration for your specific dataset. Techniques like grid search or randomized search can be helpful for this process.
3. Visualization: Visualize the UMAP embedding to gain insights into the structure of the data and to identify any potential issues with the embedding.
4. Validation: Evaluate the quality of the UMAP embedding using appropriate metrics and compare it to other dimensionality reduction techniques.

Conclusion: Unlocking the Power of Neighborhoods

UMAP’s use of nearest neighbors provides a robust and intuitive approach to dimensionality reduction. By capturing the local and global structure of the data, UMAP creates faithful low-dimensional representations that preserve essential relationships. This ability to unlock the hidden patterns within complex datasets makes UMAP a powerful tool for a wide range of applications, from data visualization and exploration to clustering, anomaly detection, and more. By understanding the concept of nearest neighbors and the mechanics of UMAP, researchers and analysts can leverage this powerful technique to gain deeper insights from their data.

Closure

Thus, we hope this article has provided valuable insights into Unlocking the Power of Dimensionality Reduction: Understanding UMAP’s Neighborhoods. We appreciate your attention to our article. See you in our next article!